As the second and final assignment for the Structured Inquiry course I’m taking with New Visions, I was asked to create a task using the Connection Representations instructional routine (#ConnectingReps). More on Instrutional Routines here.
The instructor, Kaitlin Ruggiero, mentioned that multiple choice questions are good starting points for developing these tasks. Adopting her suggestion, I used #4 from the June 2016 Algebra 2 Regents Exam. The question focuses on roots and end behavior of a function. (F.IF.8). I chose to narrow my focus to strictly end behavior.
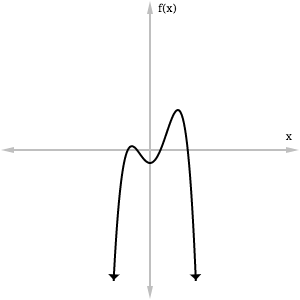
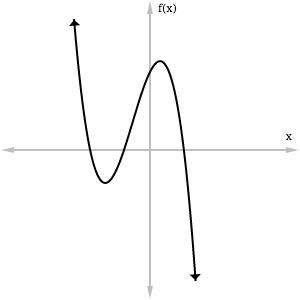
Here are the first set of representations, graphs of several polynomial functions:
Here are the second set of representations, statements about the end behavior of each graph:
During rehearsal, I showed graphs A, B, and D and their corresponding end behavior statements. We followed the routine to match the representations. I then revealed graph C and had them come up with the statement, which is 4. Lastly, the class reflected on what they learned using meta-reflection prompts.
I don’t have a formal write-up of the activity, but here are the above images.
Reflections:
- I designed this for my algebra 2 class. My gut is telling me that it may fit in well at the beginning of my rational and polynomial functions unit. I may also consider using it if/when we review domain and range.
- Initial noticings about the graphs had more to do with the “inner behavior” rather than the end behavior. In other words, the class was drawn to the minima, maxima, and roots.
- There was some blank stares when I revealed the statements. This will most likely happen with students, too. The mapping symbol (i.e. function arrow) can be confusing if you’ve never seen it before. But that was the point.
- Most of the class chunked all of the “x approaches…” statements and realized that they were the same in each representation. Since two of the given graphs (A and B) had both ends going to either positive or negative infinity and the other graph (D) didn’t, this led them to conclude that graph D had to match with statement 2. From there they reasoned that since graph A is going up on both ends, it should match with statement 1. Similar reasoning was used to match graph C with statement 4.
- By giving the class three graphs and three statements, the third match (C and 4) was kind of boring. I still made them justify why C and 4 matched, but it didn’t feel as meaningful.
- In retrospect, I wouldn’t change any of the representations, but I would revise what I give the class and what I have them construct on their own in order to help them move between representations more fluidly:
- Give only A and B and their matching statements (1 and 3). Students reason through the matches.
- Then give graph C and have them construct the corresponding statement (which is statement 4).
- As an extension, I would give statement 2 and have them sketch a graph that goes with it. All student graphs will be similar to graph D, but the “inner behavior” will be all over the place. Because of the infinite number of possible correct responses, we could show several graphs under the Elmo to guide this part of the routine. I could save these student-generated graphs for later analysis on other properties, including even/odd, roots, maxima/minima, etc.
- I didn’t use the words chunk, change, or connect at any point during the rehearsal. This is somewhat disappointing since I want my students to use these terms to describe their reasoning during this routine. Mental note taken.
- Instead of me selecting the next presenter, sometimes I should allow the student that just presented to choose. This is student-centric and I like it (when appropriate).
- Compared to Contemplate then Calculate, I feel that Connecting Representations is a slightly more complex in nature. With that said, Connecting Representations uses matching, which is really user-friendly. Both routines emphasize mathematical structure, but it seems to me like Connecting Representations emphasizes structure between different representations while Contemplate then Calculate focuses on structure within a representation. Dylan Kane and Nicole Hansen hinted at this during TMC16.
- Though I didn’t use Connecting Representations, this past spring I foreshadowed this work with my Sigma notation lesson. Given two representations (sigma notation and its expanded sum), students used reasoning to connect the two.
- This in-depth experience with both of these routines will allow my students to surface and leverage mathematical structure through inquiry like never before. So exciting!
bp






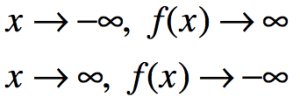
This looks like a great activity, Brian! I’m also thinking it might be a nice way to introduce limit notation (both left/right/at a point and to infinity–maybe in separate lessons) in Precal as well!
LikeLike
True. I think there was a mention of that during class. Good call!
LikeLike